Table des matières
Clapping Music for Robots
Contexte
Connaissez-vous Steve Reich ? Il s'agit d'un fabuleux musicien classique du XXe siècle, qui retravaille la question du son après l'aporie du dodécaphonisme. Contrairement aux conneries qu'a composé Schönberg, c'est intelligent, mais en plus, c'est agréable à écouter.
Une étudiante de l'ESAD m'a sollicité pour mettre en place une version robotisée de la pièce Clapping Music, dont voici une partition :
L'idée musicale
Comme vous pouvez le voir si vous avez appris à lire les grappes de cerises, il s'agit d'un jeu polyrythmique assez simple à conceptualiser (mais v'là comme c'est chaud à jouer) :
Une clave de x temps est répétée en boucle par la première voix.
Une seconde voix commence à jouer la clave de manière synchrone. Tous les Y cycles, la seconde voix “omet” un temps, ce qui décale la clave par rapport à la première voix.
De fait, tous les X * Y cycles, les deux voix finissent par se recaler l'une l'autre.
Première mesure
L'étudiante souhaite utiliser un Arduino afin de piloter deux servomoteurs qui jouent les deux voix mentionnées ci-dessus.
Dans sa première version, elle a eu une idée géniale : déclarer deux boucles différentes pour chacun des servos, et indiquer de manière brute la partition en assignant les temps d'attentes à l'aide de la fonction delay() .
Malheureusement, cette manière de faire nécessite de taper 4 lignes de code par note et par voix, soit, ben en fait, beaucoup trop de lignes.
Plus grave encore, il n'est en fait pas possible de déclarer deux boucles différentes dans l'Arduino ! Cela impliquerait du multithreading, et la puce n'a qu'un cœur…
L'étudiante, qui a décidément une âme de hackeuse, a donc intuitionné qu'elle pouvait utiliser deux Arduinos pour créer la polyrythmie. C'est en effet faisable, mais peut-être un peu too much… De plus, je suspecte qu'ils se désynchronisent assez rapidement, rendant la pièce inaudible.
Partition à raie
Je lui ai donc pointé du doigt quelque chose de presque magique : il est possible de considérer une Array comme une partition.
Si nous prenons l'exemple suivant :
[ 1, 0, 0, 1, 0, 0, 1, 0 ]
On peut y voir une représentation d'une partition rythmique représentant la clave ||: Noire pointée - Noire pointée - Noire :|| si l'on itère régulièrement dessus, ne jouant une note que si l'index est égal à 1.
On peut étendre ce principe plus loin, en modifiant le décodeur pour réagir au contenu de l'Array, par exemple :
Un séquenceur probabiliste :
[ 1, 0, 0.5, 1, 0, 0.5, 1, 0.25 ]
Ou des durée de notes :
[ 1, 0, 0.5, 1, 0, 0.5, 1, 0.25 ]
Mais du coup, pas les deux en même temps si le contenu de l'Array est une valeur seule (sinon on met des Arrays dans l'Array).
Un dernier exemple, la basse d'Alberti, en Do, en MIDI :
[ 60, 67, 64, 67 ]
écalageD
Dans cette optique, j'ai indiqué à l'étudiante que la meilleure manière de faire était de stocker la clave initiale dans une Array, puis de déclarer une seconde Array qui serait reconstruite à chaque fin de cycles pour représenter la nouvelle partition de la voix II.
Elle m'a rétorqué qu'en fait, vu qu'on accède à l'Array par un index, il suffisait de décaler cet index pour décaler la partition…
Ce qui est tout-à-fait vrai, et même pertinent en terme algorithmique. Cela pose un problème de dépassement car le décalage demandera à un moment d'accéder à un index supérieur à la taille de l'Array, mais ce problème se règle assez facilement (nous le verrons par la suite).
Cependant, je lui ai conseillé dans un premier temps de reconstruire la seconde voix de manière algorithmique pour que l'Array de la seconde voix corresponde effectivement à chaque instant à la partition réellement jouée par cette voix.
Représentation
Cette orientation était avant tout didactique : je pense qu'il est mieux d'apprendre en premier lieu à résoudre concrètement un problème équivalent à sa représentation conceptuelle, avant d'ajouter un hack.
Je laisse ici de côté la solution de reconstruction de la bonne partition à chaque changement pour me concentrer sur les solutions alternatives, qui nous éloignent de la manière dont on conçoit la partition habituellement.
La première solution pour résoudre le problème est la suivante :
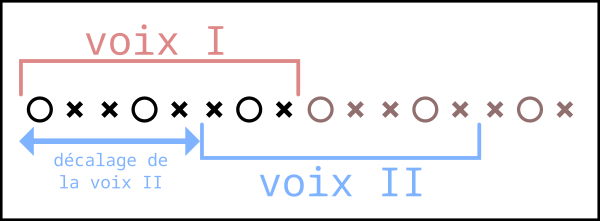
Nous commençons par dupliquer notre partition :
Si vous y réfléchissez, la dernière note est d'ailleurs superflue.
Maintenant, voici comme est décrite notre partition en terme algorithmique :
À chaque fin de cycles, on augmente le décalage de la seconde voix, et on le remet à zéro s'il atteint le nombre de temps de la clave initiale.
Ce qui semble étrange, c'est que cette méthode introduit une asymétrie de représentation des deux voix. Une information supplémentaire est nécessaire pour situer la voix II : son décalage par rapport à l'origine.
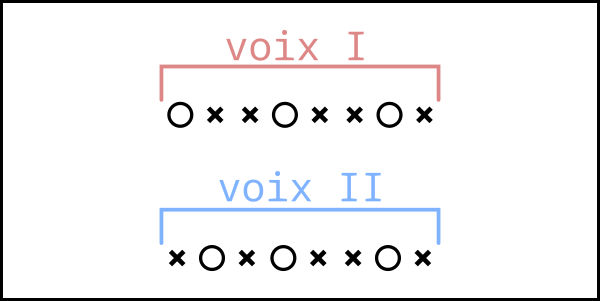
Ce n'est pas le cas avec la représentation “reconstruite” :
Les deux font pourtant référence au même objet. La première solution est efficiente en terme de calcul. La seconde est plus facile à comprendre pour les humains.
Voici le code associé à cet algorithme, qui, à la place de servomoteurs, fait clignoter des LEDs :
int ledPin1 = 2;
int ledPin2 = 3;
int msBetweenBeats = 200;
int initialScore[] = { 1, 0, 0, 1, 0, 0, 1, 0 };
int score[16];
int currentBeat = 0;
int numberOfBeats;
int currentCycleRepetition = 0;
int numberOfCycleRepetitions = 4;
int currentCycle = 0;
void setup() {
Serial.begin(9600);
pinMode( ledPin1, OUTPUT );
pinMode( ledPin2, OUTPUT );
numberOfBeats = sizeof( initialScore ) / sizeof( initialScore[0] );
for( int i = 0; i < ( numberOfBeats * 2 ); i++ ) {
score[ i ] = initialScore[ i%numberOfBeats ];
};
}
void loop() {
Serial.println( score[ currentBeat + currentCycle ] );
if( score[ currentBeat ] == 1 ) {
digitalWrite( ledPin1, HIGH );
};
if( score[ currentBeat + currentCycle ] == 1 ) {
digitalWrite( ledPin2, HIGH );
};
delay( msBetweenBeats / 4 * 3 );
digitalWrite( ledPin1, LOW );
digitalWrite( ledPin2, LOW );
delay( msBetweenBeats / 4 );
currentBeat = currentBeat + 1;
if( currentBeat == numberOfBeats ) {
currentBeat = 0;
currentCycleRepetition = currentCycleRepetition + 1;
if( currentCycleRepetition == numberOfCycleRepetitions ) {
currentCycleRepetition = 0;
currentCycle = currentCycle + 1;
if( currentCycle == numberOfBeats ) {
currentCycle = 0;
};
};
};
}
Physiologie ?
Pour aller encore plus loin, il faut noter que le duplicata de l'Array n'est même pas nécessaire.
Avec cet algorithme, il n'est même plus possible de représenter adéquatement la “partition” de la deuxième voix à l'aide d'un dessin, puisqu'elle est dépendante de l'utilisation du modulo (%) qui est une opération logique effectuée sur des électrons :
noteAcutelleDeLaDeuxièmeVoix = score[ ( currentBeat + currentCycle ) % numberOfBeats ];
Encore une fois pourtant, l'effet réel est le bon et les LEDs jouent en rythme.
Cela nous questionne sur la définition de la partition.
Doit-elle être considérée comme un système de symbole purement informatifs, ou comme un objet agissant sur le musicien de telle sorte à le faire jouer correctement ?
La version “reconstruite” à l'aide de deux Arrays semble pencher du première côté, étant très descriptive, même si l'inspection du contenu des Arrays agit effectivement sur les LEDs. Cela n'est cependant pas immédiat : la partition est d'abord “écrite”, puis “lue” a posteriori pour déclencher le clignotement.
À l'inverse, dans le cas de la version “modulo” de l'algorithme, nous sommes beaucoup plus proche de la seconde hypothèse. Ici, l'algorithme ressemble plus à une description de la manière dont le corps doit se comporter pour jouer la partition. La partition est en quelque sorte “cachée” dans l'algorithme, et bien qu'elle puisse être déduite de l'algorithme, elle n'est pas accessible de manière immédiate. Par ailleurs, contrairement au premier exemple, il n'y a aucune information donnée a priori, et l'Arduino a sa propre méthode pour savoir trouver la note qu'il doit jouer au moment même où il doit la jouer.
int ledPin1 = 2;
int ledPin2 = 3;
int msBetweenBeats = 200;
int score[] = { 1, 0, 0, 1, 0, 0, 1, 0 };
int currentBeat = 0;
int numberOfBeats;
int currentCycleRepetition = 0;
int numberOfCycleRepetitions = 4;
int currentCycle = 0;
void setup() {
Serial.begin(9600);
pinMode( ledPin1, OUTPUT );
pinMode( ledPin2, OUTPUT );
numberOfBeats = sizeof( score ) / sizeof( score[0] );
}
void loop() {
Serial.println( score[ currentBeat + currentCycle ] );
if( score[ currentBeat ] == 1 ) {
digitalWrite( ledPin1, HIGH );
};
if( score[ ( currentBeat + currentCycle ) % numberOfBeats ] == 1 ) {
digitalWrite( ledPin2, HIGH );
};
delay( msBetweenBeats / 4 * 3 );
digitalWrite( ledPin1, LOW );
digitalWrite( ledPin2, LOW );
delay( msBetweenBeats / 4 );
currentBeat = currentBeat + 1;
if( currentBeat == numberOfBeats ) {
currentBeat = 0;
currentCycleRepetition = currentCycleRepetition + 1;
if( currentCycleRepetition == numberOfCycleRepetitions ) {
currentCycleRepetition = 0;
currentCycle = currentCycle + 1;
if( currentCycle == numberOfBeats ) {
currentCycle = 0;
};
};
};
}